Diferansiyel, matematik ve mühendislik alanlarında kritik bir öneme sahip olan temel bir kavramdır. Peki, diferansiyel nedir ve neden bu kadar önemlidir? Bu yazıda, diferansiyelin tanımını, matematiksel temellerini ve uygulama alanlarını derinlemesine inceleyeceğiz. Ayrıca, diferansiyel hesaplamada kullanılan temel kurallar ve geometrik yorumları da ele alacağız. Amacımız, okuyucuların diferansiyelin çeşitli boyutlarını anlamalarına yardımcı olmaktır.
Diferansiyelin Tanımı ve Önemi
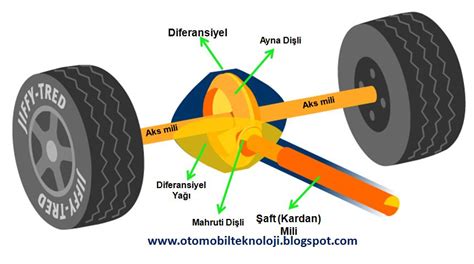
Diferansiyel, matematikte ve fiziksel bilimlerde önemli bir kavramdır. Temel olarak, bir fonksiyonun değişim oranını ifade eder. Yani, bir değişkenin küçük bir değişiminde, diğer değişkenin ne kadar değiştiğini gösterir. Diferansiyel nedir sorusunun cevabı, genellikle şöyle açıklanabilir:
- Bir fonksiyonun türevidir: Belirli bir noktadaki eğimi belirler.
- Değişim oranı sağlar: Sürekli değişen durumların analizinde kullanılır.
Diferansiyelin önemi, birçok alanda ortaya çıkar:
- Fizik: Hareket, hız ve ivme hesaplamalarında kritik rol oynar.
- Ekonomi: Marjinal analizde, maliyet ve gelir değişimlerini anlamak için kullanılır.
- Mühendislik: Yapı tasarımı ve sistem analizinde diferansiyel denklemlerle çalışılır.
Diferansiyel nedir sorusu, birçok disiplinde temel bir anlayış geliştirmenize yardımcı olur. Çünkü diferansiyel, karmaşık sistemlerin ve süreçlerin incelenmesinde vazgeçilmez bir araçtır. Kısacası, canlı sistemler ve mühendislik uygulamalarında diferansiyel, değişim ve etkileşimlerin anlaşılmasını sağlar.
Diferansiyelin Matematiksel Temelleri
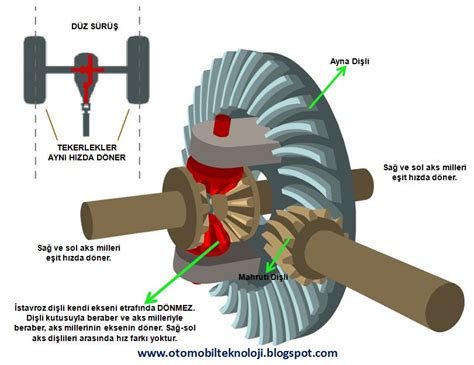
Diferansiyel nedir? Matematikte, diferansiyel kavramı, fonksiyonların değişim hızlarını incelemek için kullanılan temel bir araçtır. Çeşitli matematiksel prensipler ile desteklenen diferansiyalar, özellikle kalkülüs alanında büyük bir öneme sahiptir. İşte diferansiyelin matematiksel temellerine dair bazı temel noktalar:
Limit Kavramı: Diferansiyelin tanımında limit, temel bir rol oynar. Bir fonksiyonun bir noktadaki diferansiyelini bulmak için o noktaya yaklaşırken fonksiyon değerinin değişim oranını incelemek gerekir.
Türev Kavramı: Diferansiyelin en önemli unsurlarından biri türevidir. Türev, bir fonksiyonun belirli bir noktadaki eğimini veya değişim hızını gösterir. Matematiksel olarak, bir ( f(x) ) fonksiyonunun türevi genellikle ( f'(x) ) veya ( \frac{df}{dx} ) olarak ifade edilir.
Diferansiyel Notasyonu: Diferansiyel, genellikle ( dy ) ve ( dx ) notasyonları ile ifade edilir. Burada ( dy ), ( y ) değişkenindeki küçük bir değişimi; ( dx ), ( x ) değişkenindeki küçük bir değişimi temsil eder.
Türev ve Diferansiyel Arasındaki İlişki
| Özellik | Türev | Diferansiyel |
|---|---|---|
| Tanım | Bir fonksiyonun eğimi | Fonksiyondaki küçük değişim |
| Kullanım | Maksimum/minimum bulma | Fonksiyonun eğim hesaplama |
| Notasyon | ( f'(x) ) veya ( \frac{df}{dx} ) | ( dy = f'(x)dx ) |
Sonuç olarak, diferansiyelin matematiksel temelleri, limit ve türev kavramları üzerine inşa edilmiştir. Diferansiyel nedir sorusunun cevabı, bu kavramların iyi anlaşılmasıyla daha net hale gelir.
Diferansiyelin Kullanım Alanları

Diferansiyel nedir sorusu, matematiksel dünyada önemli bir yere sahiptir. Diferansiyel, birçok alanda uygulama bulur ve bu uygulamalar günlük yaşamdan mühendisliğe kadar geniş bir yelpazede yer alır. İşte bu alanların bazıları:
Fizik: Hareket, hız ve ivme gibi kavramların analizi için diferansiyelden faydalanılır. Örneğin, bir cismin hızının zamanla nasıl değiştiğini anlamak için türev kullanılır.
Mühendislik: Yapıların dayanıklılığını değerlendirmede, akışkan dinamiği ve elektrik devreleri gibi konularda diferansiyel denklemler önemli rol oynar.
Ekonomi: Ekonomik modellerin analizi ve optimizasyonu için diferansiyel kavramlarının kullanımı yaygındır. Özellikle marjinal analizde, üretim ve tüketim değişimlerini incelemek için kullanılır.
Biyoloji: Popülasyon dinamikleri ve yayılma modelleri gibi konularda diferansiyel eşitlikler, biyolojik süreçlerin anlaşılmasında kritik bir öneme sahiptir.
Bilgisayar Bilimleri: Veri analizi ve makine öğreniminde, algoritmaların ve modellemelerin geliştirilmesinde diferansiyel yöntemler kullanılmaktadır.
Diferansiyelin kullanıldığı bu alanlar, matematiksel teorilerin gerçek dünya problemlerini çözmede ne kadar etkili olduğunu göstermektedir. Bu nedenle, diferansiyel nedir sorusuna verilecek yanıtlar, yalnızca matematiksel bir kavramı değil, aynı zamanda çok çeşitli disiplinlere yayılan bir uygulama alanını da kapsar.
Diferansiyel Hesaplamada Temel Kurallar

Diferansiyel hesaplama, bir fonksiyonun değişim oranını inceleyen matematiksel bir alandır. Bu alanda bazı temel kurallar, hesaplamaların doğru ve etkili bir şekilde yapılmasını sağlar. Peki, diferansiyel nedir sorusunu daha iyi anlamak için bu kuralları inceleyelim.
1. Toplama Kuralı
Eğer ( f(x) ) ve ( g(x) ) iki fonksiyon ise,
- ((f + g)'(x) = f'(x) + g'(x))
2. Çıkarma Kuralı
Benzer şekilde,
- ((f – g)'(x) = f'(x) – g'(x))
3. Çarpma Kuralı
İki fonksiyonun çarpımının türevi,
- ((f \cdot g)'(x) = f'(x)g(x) + f(x)g'(x))
4. Bölme Kuralı
Bölme işlemi için ise,
- (\left(\frac{f}{g}\right)'(x) = \frac{f'(x)g(x) – f(x)g'(x)}{(g(x))^2})
5. Zincir Kuralı
Fonksiyonların bileşimi için,
- ((f(g(x)))’ = f'(g(x)) \cdot g'(x))
Bu kurallar, diferansiyel nedir sorusunun belirleyici unsurlarındandır. Uygulamalarında bu kuralları kullanmak, problemleri daha hızlı ve sistematik bir şekilde çözmemizi sağlar. Matematiksel anlamda sağlam bir temel oluşturur, böylece ileri düzey diferansiyel konulara geçişi de kolaylaştırır.
Diferansiyelin Geometrik Yorumları

Diferansiyelin geometrik yorumları, matematiksel kavramların daha iyi anlaşılmasına yardımcı olur. Özellikle bir fonksiyonun davranışını grafikte görmek, diferansiyelin nedir sorusunun daha net bir cevap bulmasına olanak tanır. İşte diferansiyelin geometrik açılımlarını inceleyen bazı anahtar noktalar:
Türev ve Eğim İlişkisi:
- Bir fonksiyonun türevi, o noktadaki eğimi temsil eder. Yani,
f'(x)ifadesi,f(x)fonksiyonununxnoktasındaki eğimini gösterir.
- Bir fonksiyonun türevi, o noktadaki eğimi temsil eder. Yani,
Türev ve Teğet Doğru:
- Türev, bir fonksiyonun o noktada çizilen teğet doğrunun eğimini verir. Bu durum, diferansiyelin nedir sorusunun somut bir yanıtıdır.
Küçük Değişiklikler:
- Diferansiyel, bir fonksiyondaki küçük değişimlerin, sonuçta ne kadar değişiklik yarattığını ortaya koyar. Bu,
dy/dxolarak ifade edilir.
- Diferansiyel, bir fonksiyondaki küçük değişimlerin, sonuçta ne kadar değişiklik yarattığını ortaya koyar. Bu,
Örnek:
Aşağıdaki tablo, bir fonksiyonun farklı noktalarındaki türev değerlerini gösterir:
| Nokta (x) | Fonksiyon (f(x)) | Türev (f'(x)) | Teğet Doğru Eğimi |
|---|---|---|---|
| 1 | 2 | 3 | 3 |
| 2 | 4 | 5 | 5 |
| 3 | 6 | 1 | 1 |
Sonuç olarak, diferansiyelin nedir sorusuna yanıt ararken, bu geometrik yaklaşımlar, matematiksel kavramların görselleştirilmesine yardımcı olur ve türevlerin ne anlama geldiğini daha iyi anlamamızı sağlar.
Diferansiyel Eşitlikler ve Uygulamaları
Diferansiyel eşitlikler, matematiğin önemli bir dalını oluşturarak, birçok alanda geniş uygulama fırsatları sunmaktadır. Peki, diferansiyel nedir ve bu eşitlikler nerelerde kullanılır?
Diferansiyel Eşitliklerin Temel Tanımı
Diferansiyel eşitlik, bir fonksiyonun türevini veya türevlerinin ilişkilerini içeren matematiksel bir ifadedir. Örneğin, bir fonksiyon y‘nin birinci türevi y’ ile ifade edilebilir. Bu tür eşitlikler çoğunlukla iki gruba ayrılır:
- Normal Diferansiyel Eşitlikler: Tek bağımsız değişken içeren eşitliklerdir.
- Kısmi Diferansiyel Eşitlikler: Birden fazla bağımsız değişken içeren eşitliklerdir.
Uygulama Alanları
Diferansiyel eşitlikler, aşağıdaki alanlarda sıkça kullanılır:
- Fizik: Hareket denklemleri ve enerji hesaplamaları.
- Mühendislik: Sistemlerin kontrolü ve analizi.
- Ekonomi: Büyüme modelleri ve optimizasyon problemleri.
- Biyoloji: Popülasyon dinamikleri ve epidemiyoloji.
| Uygulama Alanı | Açıklama |
|---|---|
| Fizik | Doğal olayların matematiksel modellemesi |
| Mühendislik | Teknolojik sistemlerin analizi ve geliştirilmesi |
| Ekonomi | Ekonomik büyüme ve mali politikaların incelenmesi |
| Biyoloji | Canlıların büyüme ve yayılma modellerinin analizi |
Bu bağlamda, diferansiyel nedir sorusu, birçok bilim dalında karşımıza çıkan kritik bir kavramdır. Diferansiyel eşitliklerin derinlemesine incelenmesi, çeşitli probleme uygun çözümler üretebilmeyi sağlar.
İleri Düzey Diferansiyel Konuları
İleri düzey diferansiyel konuları, diferansiyel nedir sorusunun ötesine geçerek, daha derin matematiksel kavramlar ve uygulamalara odaklanır. Bu konular genellikle diferansiyel denklemler, Jacobian matrisler, ve Türevler ile İntegrallerin İlişkisi gibi başlıkları içerir.
Bu konular arasında en yaygın olanları şunlardır:
Diferansiyel Denklemler:
- Birinci Dereceden: Basit bir değişkenin türevini içeren denklemler.
- İkinci Dereceden ve Üstü: Daha karmaşık sistemler ve çoğu fiziksel fenomenler için kullanılır.
Jacobian Matrisler:
- Çok değişkenli fonksiyonların türevini hesaplamada kullanılır.
- Sistemlerin stabilitesini analiz etmek için önemli bir araçtır.
Türev ve İntegral İlişkileri:
- Fundamental Theorem of Calculus: Türev ve integralin birbirine nasıl bağlı olduğunu gösterir.
- Analitik çözümleme yöntemleri, ileri düzey hesaplamalarda kritik öneme sahiptir.
Bu kavramlar, ses ve ışık dalgalarının modellemesi gibi karmaşık sistemlerin anlaşılmasında ve mühendislik uygulamalarında sıklıkla kullanılmaktadır. Sonuç olarak, diferansiyel nedir sorusunu derinleştiren bu ileri düzey konular, matematiğin temel dinamiklerini anlamak için hayati öneme sahiptir.
Diferansiyel Eğitimi ve Kaynaklar
Diferansiyel nedir sorusunu anlamak için doğru eğitim ve kaynakları kullanmak büyük önem taşır. Diferansiyel hesaplama, matematikteki en temel konulardan biridir ve çeşitli alanlarda uygulama imkanı sunar. Bu nedenle, öğrenmek isteyenler için aşağıdaki kaynaklar oldukça faydalıdır:
- Online Eğitim Platformları: Coursera, edX ve Udemy gibi platformlar, diferansiyel hesaplama konusunda kapsamlı kurslar sunar. İleri düzey konular ve temel bilgiler için iyi bir başlangıç noktasıdır.
- Üniversite Ders Kitapları: "Calculus" ve "Differential Equations" gibi klasik kitaplar, diferansiyel nedir sorusunu derinlemesine ele alır. Özellikle James Stewart ve Thomas’ı öneririz.
- Video Dersler: YouTube, matematik eğitimi için oldukça zengin bir kaynaktır. Khan Academy ve 3Blue1Brown gibi kanallar, diferansiyel hesaplama konularını görsel ve işitsel olarak öğretir.
- Uygulamalar ve Yazılımlar: Wolfram Alpha ve GeoGebra gibi araçlar, diferansiyel hesaplama problemlerini çözmekte yardımcı olabilir. Bu tür uygulamalar sayesinde teorik bilgilerinizi pratiğe dökebilirsiniz.
Ayrıca üniversitelerin düzenlediği seminerler ve atölyeler, alana dair güncel bilgilere ulaşmak açısından büyük avantaj sağlar. Diferansiyel nedir sorusunun yanıtını yalnızca kitaplardan öğrenmekle kalmayıp, aynı zamanda etkileşimli öğrenim yöntemlerini de kullanarak pekiştirmek önemlidir.
Sıkça Sorulan Sorular
Diferansiyel nedir?
Diferansiyel, matematikte bir değişkenin, bir fonksiyonun bir noktada nasıl değiştiğinin ölçüsüdür. Daha basit bir ifadeyle, diferansiyel, bir fonksiyonun eğimini veya eğim değişimini belirlemek için kullanılan bir kavramdır. Bu kavram, özellikle analiz ve hesaplamalarda önemli bir rol oynamaktadır, çünkü fonksiyonların maksimum ve minimum noktalarını bulmak için kullanılır.
Diferansiyel nasıl hesaplanır?
Diferansiyel hesaplama, bir fonksiyonun ‘fünksiyonun türevi’ adı verilen matematiksel bir kavramla gerçekleştirilir. Bir fonksiyonun türevi, o fonksiyonun belirli bir noktadaki eğimini temsil eder. Türev hesaplamak için genellikle limit kavramı kullanılır. Bu süreç, belirli bir ‘h’ değeri sıfıra yaklaşırken, fonksiyonun değerinin değişim oranını bulmayı içerir.
Diferansiyelin günlük hayattaki kullanımları nelerdir?
Diferansiyel, birçok alanda yaygın olarak kullanılır. Mühendislikte gerilme ve deformasyon analizi, ekonomi alanında ise maliyet ve kar farklılıklarının hesaplanması için önemlidir. Fizikte hareket halindeki nesnelerin hız ve ivme hesaplamalarında diferansiyel hesaplama temel bir araçtır. Bu nedenle, diferansiyel kavramı bir çok sektörde kritik işlevler üstlenmektedir.
Diferansiyel ile integral arasındaki ilişki nedir?
Diferansiyel ile integral, matematikteki kalkülüsün iki temel bileşenidir. Diferansiyel, fonksiyonun yerel değişim oranını inceleyerek, eğim ile ilgilidirken, integral ise bir fonksiyonun toplam değerini veya alanını bulmakla ilgilenir. Bu iki kavram, temel teoremi ile bağlanmıştır; bu teorem, bir fonksiyonun türevini almanın, o fonksiyonun integralini almanın ters işlemi olduğunu belirtir.
Diferansiyel denklemler nedir?
Diferansiyel denklemler, bilinmeyen bir fonksiyonun ve türevlerinin birbirleriyle ilişkisini ifade eden matematiksel denklemlerdir. Bu denklemler, fizik, mühendislik, ekonomi gibi birçok alanda dinamik sistemleri modellemek için kullanılır. Örneğin, bir nesnenin hareketini veya bir popülasyonun büyüme hızını tanımlamak için diferansiyel denklemler sıklıkla başvurulan araçlardır.



